50. Pow(x, n)

题目说明

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，x^n）。

-100.0 < x < 100.0
-2^31 <= n <= 2^31-1
-10^4 <= x^n <= 10^4

示例

例1

1 2	输入：x = 2.00000, n = 10 输出：1024.00000

例2

1 2	输入：x = 2.10000, n = 3 输出：9.26100

例3

1
2
3

输入：x = 2.00000, n = -2
输出：0.25000
解释：2^-2 = 1/22 = 1/4 = 0.25

笔者理解

此题是一道数学算法问题，在力扣题库中被定义为中等题。

解法

此题中，直接暴力运算很明显是行不通的，很容易浪费大量的时间和空间，在此，我们可以把指数进行拆分，将其转化为二进制数的形式，然后用底数累乘的方式来进行计算。让我们来看看具体如何实现的吧。

实现

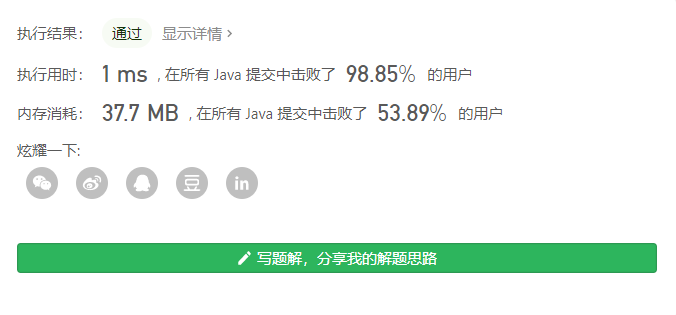
class Solution {
    public double quickMul(double x,long n) {
        double result = 1;
        double tick = x;
        //标记当前计算到的x基于二进制的次位

        while(n>0){
            //将n转化为二进制数，方便计算
            //例如 x = 3,n = 13(1101)
            //结果就等于3^1 * 3^4 * 3^8

            if(n%2==1){
                result*=tick;
                //当n在该二进制次位上有值时，累乘
            }
            tick = tick*tick;
            n/=2;
            //标记累乘
            //n向前移动
        }
        return result;
    }
    public double myPow(double x, int n) {
        long N = n;
        return N>=0?quickMul(x,N):1.0/quickMul(x,-N);
        //当n为负数时，返回x的-n次方的倒数即可
    }
}