冗余连接(java实现)

力扣 684. 冗余连接

题目说明

在本问题中, 树指的是一个连通且无环的无向图。

输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。

返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。

输入的二维数组大小在 3 到 1000。
二维数组中的整数在1到N之间，其中N是输入数组的大小。

示例

例1

输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的无向图为:
  1
 / \
2 - 3

例2

输入: [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
解释: 给定的无向图为:
5 - 1 - 2
    |   |
    4 - 3

笔者理解

此题是一道字符串判定算法问题，在力扣题库中被定义为中等题。

解法

当笔者阅读完此题后，打算用哈希表来完成此题，但发现单纯用哈希表来完成此题似乎不太可行，在题目提示中发现此题可以使用一种叫并查集的数据结构来求解，就让我们看看并查集是什么以及具体如何实现吧。

并查集

并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。

主要操作

初始化：把每个点所在集合初始化为其自身。

查找：查找元素所在的最上级，即根节点。

合并：将两个元素所在的集合合并为一个集合。

主要思路

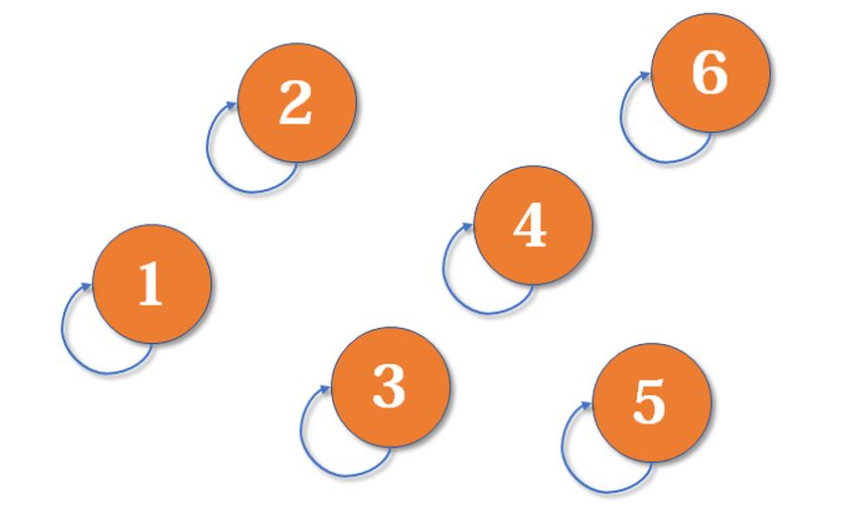
假设现在有刘一陈二张三李四王五赵六，六个人，他们相互之间是上下级关系

一开始，我们都认定自己是自己的上级；

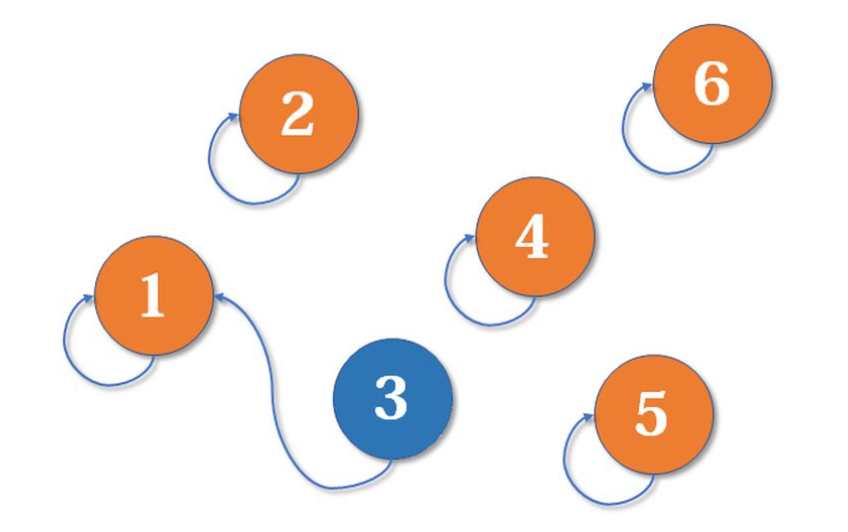
现在刘一和张三比较，张三发现，赵一的等级比自己高（此处具体谁等级高不重要），于是，张三就认定自己的上级是赵一；

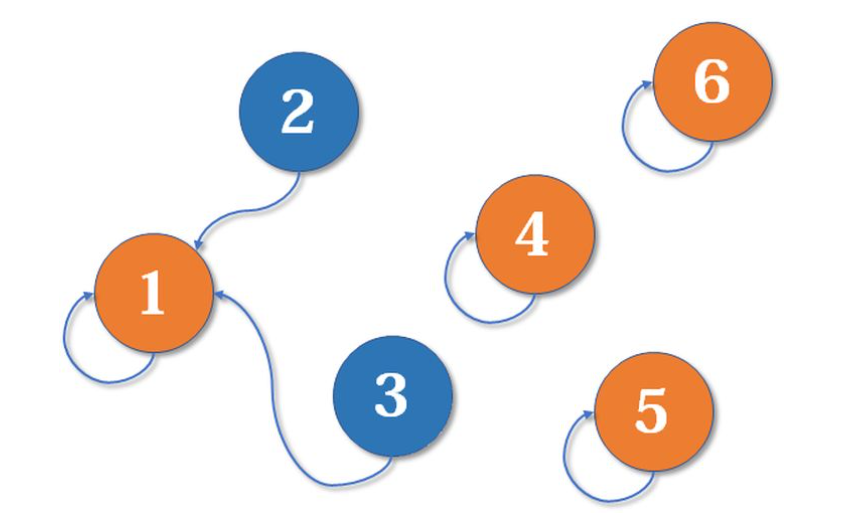
然后，陈二想要和张三比较，但是张三说：你别跟我比较，你跟我的上级去比较。假设这次还是赵一的等级比较高，于是，陈二也认定自己的上级是赵一；

之后，我们假设李四王五赵六之间也进行了一番比较，然后六个人之间的情况变成了这种情况；

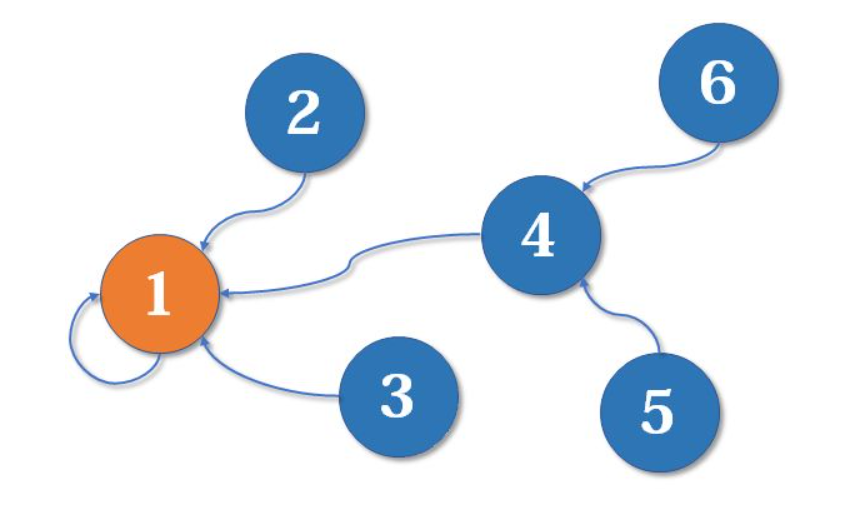
最后，假设张三想和王五比较一下，于是两位带头上级赵一和李四进行了比较，然后，赵一最终成为了所有人的最高上级了，李四手下的人员也认定了赵一是自己的上级了；

这是一个树状的结构，要寻找集合的代表元素也就是节点的上级，只需要一层一层往上访问父节点（图中箭头所指的圆），直达树的根节点（图中橙色的圆）即可。根节点的父节点是它自己。

实现

static class Disjoint{
        //定义并查集类

        int []dj;
        //用以存储各个端点的上级

        Disjoint(int n){
            //并查集构造方法，建立dj数据
            this.dj = new int[n+1];
            //因为无向图中从1开始，所以容量加一
            for (int i = 1; i < n+1; i++) {
                this.dj[i] = i;
            }
        }

        int find(int x){
            if(this.dj[x]==x){
                //如果当前节点的上级为自己就返回自己
                return x;
            }
            return find(this.dj[x]);
            //否则递归寻找最上级
        }

        void insert(int x,int y){
            this.dj[find(x)] = find(y);
            //将x的最上级的上级置为y的上级
        }
    }
    public static int[] findRedundantConnection(int[][] edges) {
        int []result = new int[2];
        //需要提出来的边
        Disjoint dis = new Disjoint(edges.length);
        //创建并查集对象
        for (int i = 0; i < edges.length; i++) {
            if(dis.find(edges[i][0])!=dis.find(edges[i][1])){
                //如果当前边的两个端点的最上级不相同，将这两个端点归并
                dis.insert(edges[i][0],edges[i][1]);
            }
            else{
                //否则将这条边提出来
                result[0] = edges[i][0];
                result[1] = edges[i][1];
                return result;
            }
        }
        return new int[2];
    }