丑数(java实现)
剑指 Offer 49 丑数
此题与力扣264题相同丑数II
题目说明
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
1是丑数。n不超过1690。
示例
例1
1 | 输入: n = 10 |
笔者理解
此题是一道数学规律问题,在力扣题库中被定义为中等题。
解法1
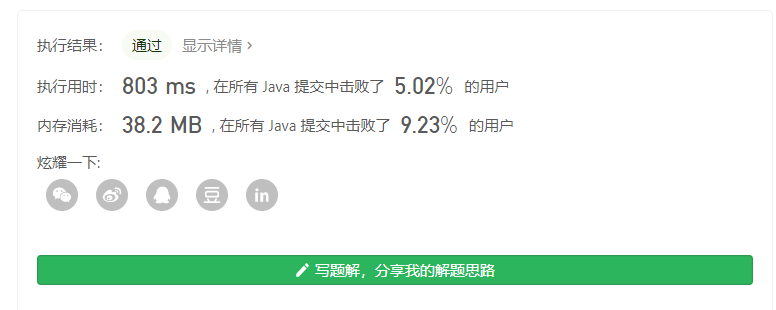
笔者思考此题时,考虑过递归及暴力求解等方法,但效果欠佳,这是通过暴力法预先将2,3,5的多种组合放入结果数组中,然后排序再去相应位置的丑数出来。
1 | public int nthUglyNumber(int n) { |
时间和空间效率都较低,此解法可以通过跳出预知的测试n对应的丑数来减少时间;
解法2
笔者偶然翻阅评论时,发现此题可以用动态规划法做,便仔细思考了以下,又实际去进行了演算,发现此题用动态规划挺合适的。
实际上,包括第一个丑数1,都是由2的i次方 x 3的j次方 x 5的k次方所得,实际上第n个丑数就是求数学表达式的第n个最小值
丑数的递推性质: 丑数只包含因子 2,3,5 ,因此有 “丑数 == 某较小丑数× 某因子”
例如:No.1 = 1 ;No.2 = 2 x No.1;No.3 = 3 x No.1(因为3 x No.1小于No.2 x 2);No.4 = No.2 x 2(因为No.2 x 2小于5 x No.1);
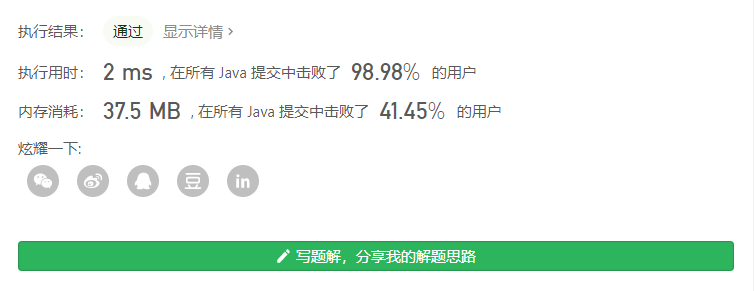
1 | public int nthUglyNumber(int n) { |
可见动态规划解法的效率很高。
总结
本题是一道中等数学算法题,感兴趣的朋友都可以去尝试一下,此题还有其他更多的解法,朋友们可以自己逐一尝试。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 徐年の博客!