旋转二维数组(java实现)

力扣48题：旋转图像

题目说明

给定一个n × n 的二维矩阵表示一个图像，将图像顺时针旋转 90 度。

说明：你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵，请不要使用另一个矩阵来旋转图像。

示例

例1

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

例2

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

笔者理解

此题是一道比较经典的二维数组题，在力扣题库中被定义为中等题，说明还是需要一定的思考的。

二维数组顺时针翻转90度，此时无法借助另一个二维数组，所以无法通过简单的替换来实现，笔者思考这个问题也思考了好一会，然后翻阅此题评论的时候发现一种奇特的方法来实现顺时针旋转，在这里与各位分享一下。

[1,2,3], 上下 [7,8,9], 对角 [7,4,1]
[4,5,6], ==> [4,5,6], ==> [8,5,2]
[7,8,9]. 翻转 [1,2,3] 交换 [9,6,3]

[1,2,3], 顺时针 [7,4,1],
[4,5,6], ===> [8,5,2],
[7,8,9]. 旋转90 [9,6,3],

先对二维数组进行上下翻转，即将第i行元素和n-1-i行元素进行置换

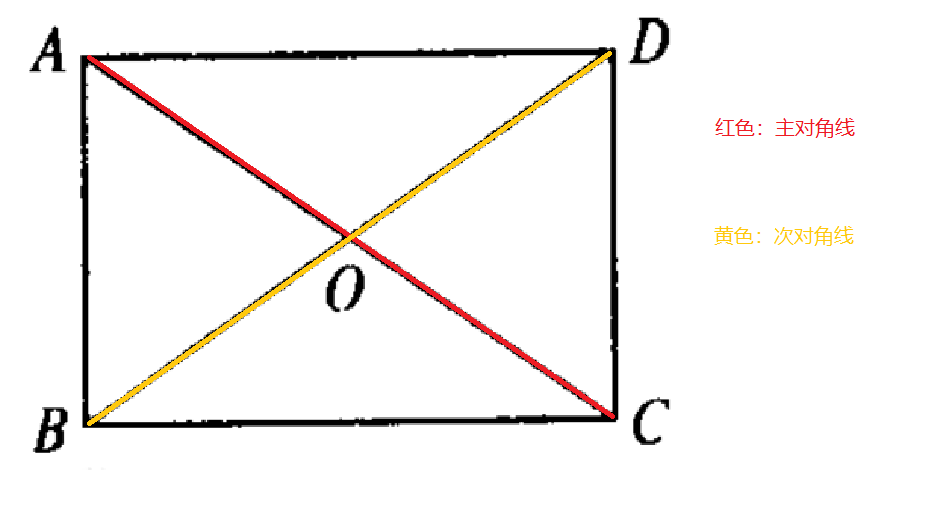
再对二维数组进行主对角线交换，即将第i行第j列的元素与第j行第i列的元素进行交换

public void rotate(int[][] matrix) {
        int temp = 0;
        int size = matrix.length;
        for(int i=0;i<size/2;i++){
            for(int j=0;j<size;j++){
                //首先将二维数组进行上下替换
                temp = matrix[i][j];
                matrix[i][j] = matrix[size-1 -i][j];
                matrix[size-1 -i][j] = temp;
            }
        }
        for(int i=0;i<size;i++){
            for(int j=i;j<size;j++){
                //再将数组进行对角替换
                temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        //实现二维数组顺时针旋转九十度
    }